
 |
| Montecarlo |
 |
| A little bit of theory |
|
Simulation with Model Analyzer for Excel uses the Monte Carlo technique. With this technique, random values are generated for the input variables so we can see their impact on output variables, thus generating thousands of parallel scenarios.
For example, if you have the variable people's height o weight, you will soon realize that most values tend towards a central value, the mean, and the farther away the values, the smaller their probability; in this case, you could use the Normal distribution. If, for example, you have the variables sales price, production costs, interest rates, and similar, each susceptible of taking three values -a minimum, a most likely and a maximum value- in this case you can use a Triangular distribution, as suggested by its name. If, on the contrary, there is no central value as in the normal distribution, but rather all values within a range have the same probability of being chosen, then you can use the Uniform distribution. Consider for example that fuel prices may range between 100 and 120 dollars the barrel in the coming two years, then the possible values 100, 101, 102, ..., 120 have the same probability of occurrence; that is, none of them is more likely to occur. To exemplify a variable that follows the Poisson distribution, consider the following case: You know, based on historical information of your company, that every customer's purchase has 1.2% chance of resulting in a complaint for any reason. Based on this data, you may analyze and determine the probability that 5 complaints will occur from 800 sales. You should think of applying Poisson here. The Poisson distribution is applicable when there is a large number of experiments or events with a very low probability of occurring. The following parameters apply: n: "number of times the experiment is performed". p: "probability of occurrence each time". The restrictions to apply Poisson are: p < 10% n * p < 10 If your input variable meets these characteristics, then you can apply Poisson. For variables with temporary growth, such as demographic variables, for example, the growth of bacteria populations- you can apply the Logistic distribution. You should use the Discrete distribution when you have variables with a definite number of probable values, and the sum of their probabitlities add up to 100%. With Model Analyzer for Excel, you will find simulations uncomplicated; the only thing you need to do is to identify the type of input variables and define their parameters, and now you're ready to perform simulations. We do not intend to give you an advance course on statistical distributions-there are plenty of books on this already that you can purchase. If this subject is new to you, it would be convenient for you to read about the types of distributions handled in this version of Model Analyzer for Excel. How to do a simulation First you have to relate the input variables involved in the experiment to the type of distribución most suitable for such variables, and enter the required parameters. In the following dialog, select the input and click the Assign the type of distribution button to assign parameters. |
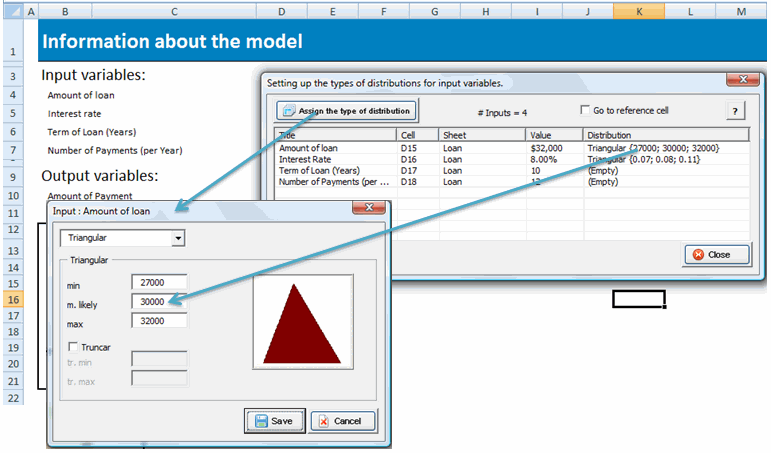 |
| The required parameters for each type of distribution are: |
 |
| The second step is to run the simulation, which prompts you to specify the number of simulations. With Model Analyzer for Excel you can complete as many as 1,000,000 simulations for each experiment. In the following case, only 1000 will be performed. |
 |
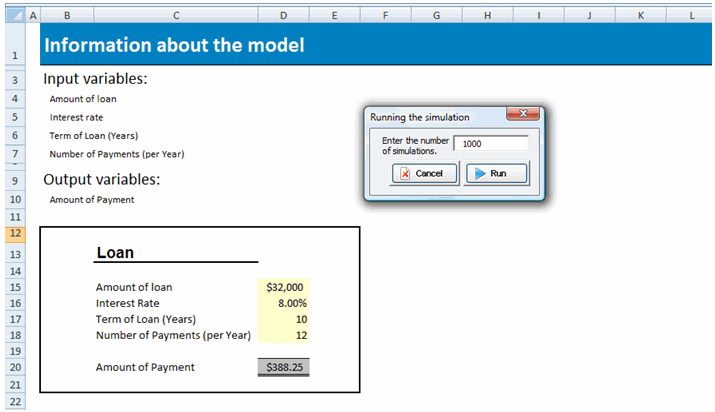 |
| Once the simulation is completed, the results are shown in a window as the following: |
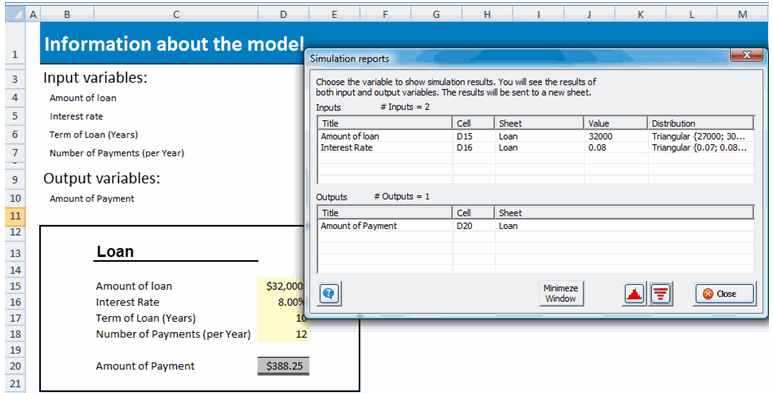 |
| Just select an output and click the |
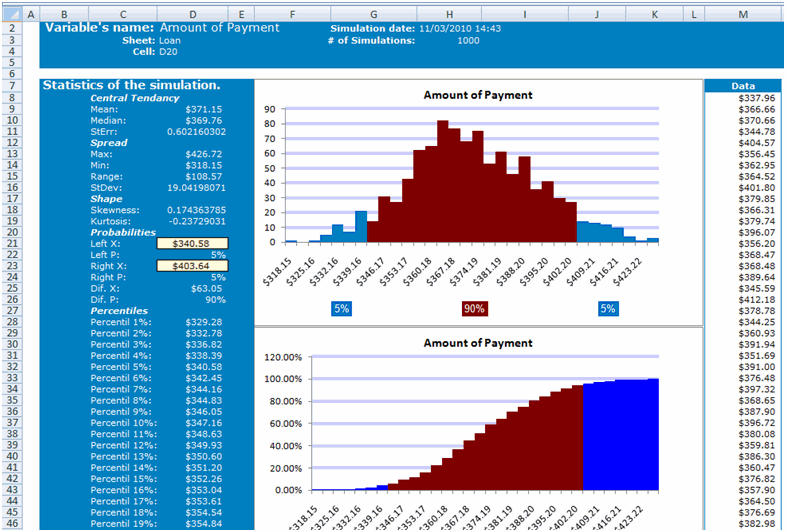 |
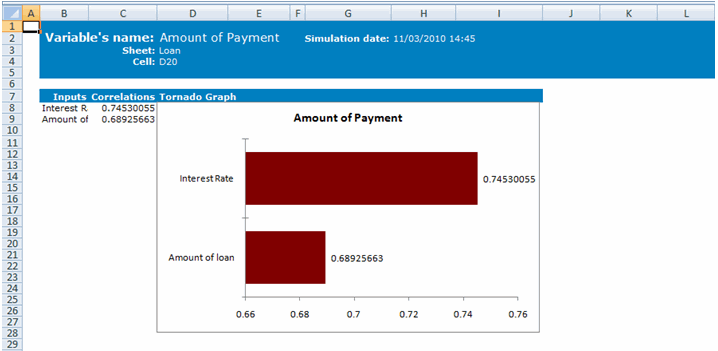
| You can also select an output and press the |
 |